非α-β算法
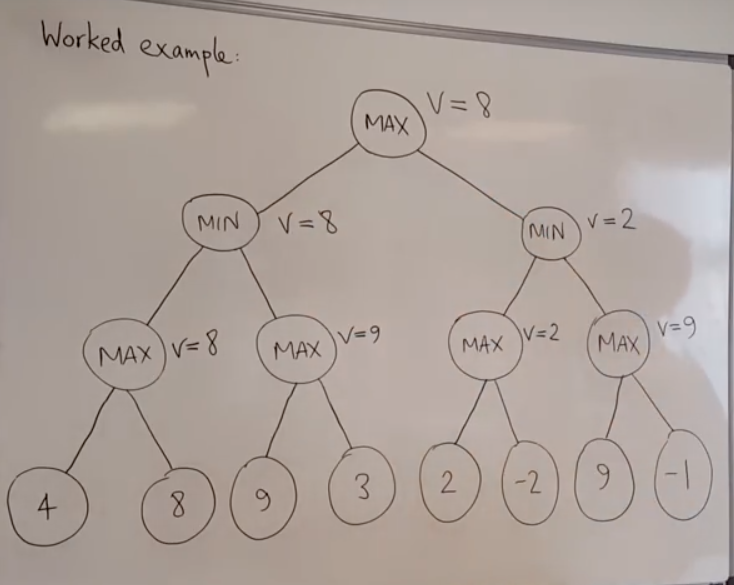
- 通过中序遍历
- MAX结点始终取当前能取的最大值
- MIN结点始终取当前能取的最小值
α-β剪枝算法
算法部分:
- MAX结点:
1
2
3
4
5
6
7
8
9
10
11
12
Max-Value(s,α,β):
if terminal(s) return U(s)
v= -Infinity
for c in next-states(s):
v' = Min-value(s,α,β) #调用Min-value函数
if v'>v: #当新的v大于原来的,则更新v
v=v'
if v'>=β: #此处即为α>β,直接剪枝,返回
return v
if v'>α: #此时新的v大于原α,则更新α
α=v'
return v
- Min结点:
1
2
3
4
5
6
7
8
9
10
11
12
Min-Value(s,α,β):
if terminal(s) return U(s)
v= +Infinity
for c in next-states(s):
v' = Max-value(s,α,β) #调用Max-value函数
if v'<v: #当新的v小于原来的,则更新v
v=v'
if v'<=α: #此处即为α>β,直接剪枝,返回
return v
if v'<β: #此时新的v小于原α,则更新α
β=v'
return v
遍历(比较像中序遍历)
- 计算孩子结点v的值,记为v’
- 比较当前的v与v’的值
- 若为MAX结点并且v’>v:v=v’
- 若为MIN结点并且v’<v:v=v’
- 将更新完的v’做替换尝试(看看v’替换α或者β后α是否还小于β,即符合条件)
- 否,则剪枝,并return v
- 是,则进行下述步骤
- 更改α、β的值(第三个if)
- 若为MAX结点并且v’>v:α=v’
- 若为MIN结点并且v’<v:β=v’
- 否则β=v’
- 重复上述步骤,直到完成整个剪枝过程(下述图片为最终效果)
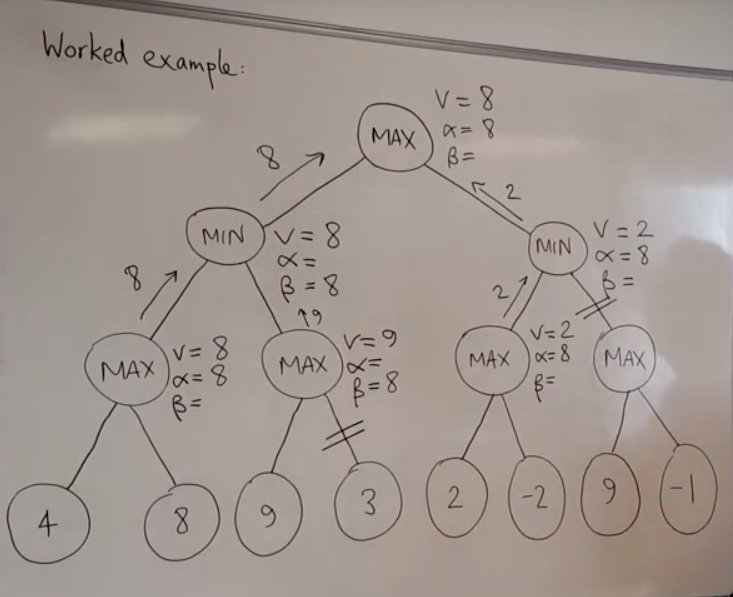
总结
1) only in a Max node can update the corresponding α,Min for β. 2) v can only be returned up to its parent 3) α and β can only be passed down from its parent 4) cut the current node from the tree whenever alpha >= beta

