Markov Chains
Markov Assumption:
\[P(q_i=a\|q_1···q_{i-1})=P(q_i=a\|q_{i-1})\]- Parameters
- $Q=q_1q_2···q_N$,用于保存状态
- $A=a_{11}a_{12}···a_{n1}···a_{nn}$,状态转移矩阵
- $\pi=\pi_1,\pi_2,···,\pi_N$,初始概率分布,指的是链式开始的状态为i的概率为$\pi_i$
The Hidden Markov Model
A Markov chain is useful when we need to compute a probability for a sequence of observable events. In many cases, however, the events we are interested in are hidden hidden: we don’t observe them directly. For example we don’t normally observe part-of-speech tags in a text. Rather, we see words, and must infer the tags from the word sequence. We call the tags hidden because they are not observed.
比Markov Chains多了2项为:
- $O=o_1o_2···o_T$,每个状态的观测值
- $B=b_i(o_t)$,表示为在 $i$ 状态下,会观测到 $o_t$ 的概率
Markov Assumption
\[P(q_i\|q_1···q_{i-1})=P(q_i\|q_{i-1})\]只与前一个状态有关
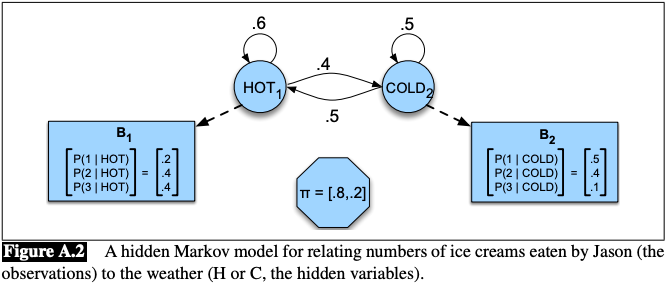
Hidden Markov Model举例
Imagine that you are a climatologist in the year 2799 studying the history of global warming. You cannot find any records of the weather in Baltimore, Maryland, for the summer of 2020, but you do find Jason Eisner’s diary, which lists how many ice creams Jason ate every day that summer. Our goal is to use these observations to estimate the temperature every day. We’ll simplify this weather task by assuming there are only two kinds of days: cold (C) and hot (H).
计算可能性:前向算法
目的:
- 计算对于一个特定观测序列存在的可能性
- 给定一个隐马可夫模型$\lambda=(A,B)$和一个观测序列,推测可能性$P(O|\lambda)$
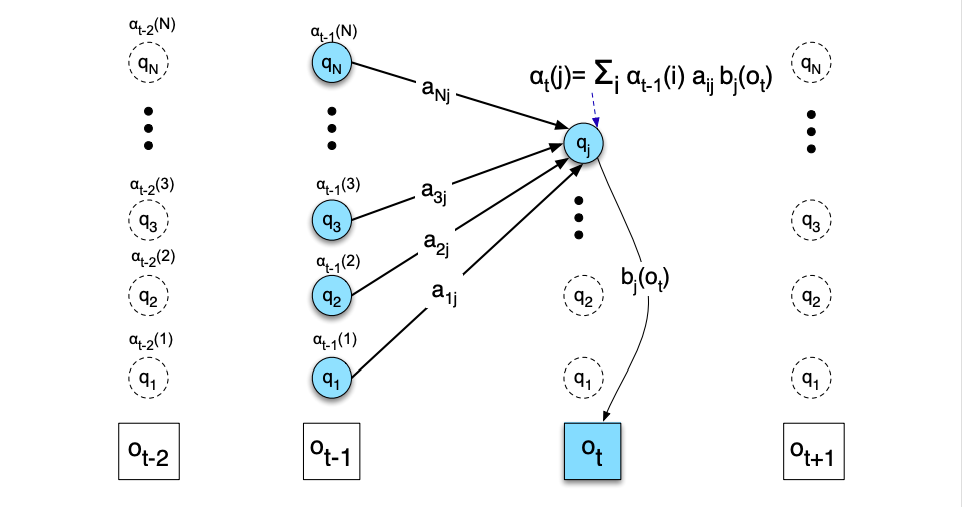
$\alpha_t(j)$为在观察到$o_t$时,状态q为$q_j$的概率
前向算法:


